sklearn应用线性回归算法
Scikit-learn 简称 sklearn 是基于 Python 语言实现的机器学习算法库,它包含了常用的机器学习算法,比如回归、分类、聚类、支持向量机、随机森林等等。同时,它使用 NumPy 库进行高效的科学计算,比如线性代数、矩阵等等。
Scikit-learn 是 GitHub 上最受欢迎的机器学习库之一,其最新版本是 2020 年12 月发布的 scikit-learn 0.24.1。
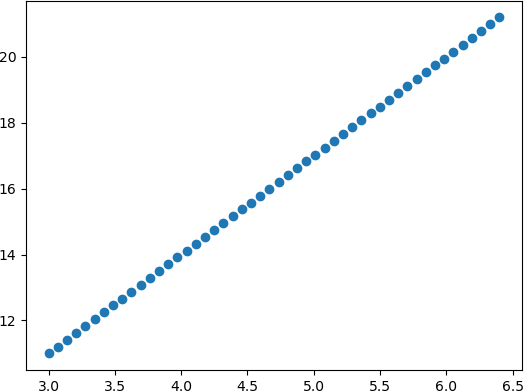
图1:线性回归函数图像
打印输出结果如下所示:
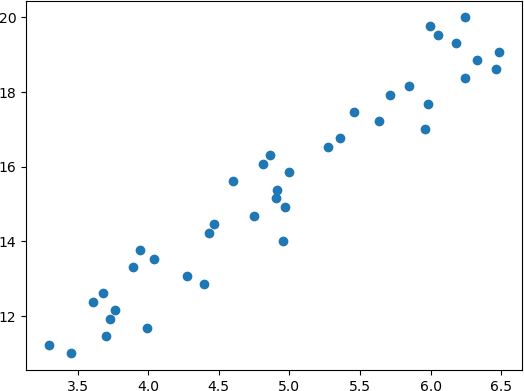
图2:修改后的散点分布
虽然做标签散乱分布,但是使用线性回归算法学习依然可以得到线性函数,此时 w 与 b 的输出结果如下所示:
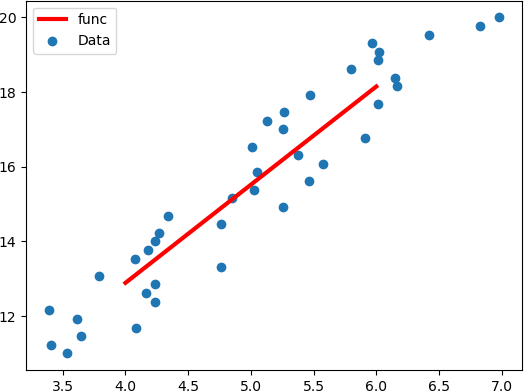
图3:拟合直线绘制
线性回归适用于有监督学习的回归问题,首先在构建线性模型前,需要准备好待输入的数据集,数据集按照需要可划分为训练集和测试集,使用训练集中的向量 X 与向量 Y 进行模型的训练,其中向量 Y 表示对应 X 的结果数值(也就是“参考答案”);而输出时需要使用测试集,输入测试 X 向量输出预测结果向量 Y。
其实线性回归主要解决了以下三个问题:
线性回归算法简单,且容易理解,但这并不影响它的广泛应用,比如经济金融领域实现股票的预测,以及著名的波士顿房价预测,这些都是线性回归的典型应有,因此我们要走出一个误区,不要感觉算法简单就不重要,机器学习虽然算法众多,但每一种算法都有其存在的理由,而掌握了线性回归就相当于拿到了算法世界的入场券。
Scikit-learn 是 GitHub 上最受欢迎的机器学习库之一,其最新版本是 2020 年12 月发布的 scikit-learn 0.24.1。
提示:Scikit-learn 官方网站:https://scikit-learn.org/stable/
Scikit-learn 涵盖了常用的机器学习算法,而且还在不断的添加完善,对于本教程所涉及的机器学习算法它都做了良好的 API 封装,以供直接调用。你可以根据不同的模型进行针对性的选择。下面介绍 sklearn 中常用的算法库:- ·linear_model:线性模型算法族库,包含了线性回归算法,以及 Logistic 回归算法,它们都是基于线性模型。
- .naiv_bayes:朴素贝叶斯模型算法库。
- .tree:决策树模型算法库。
- .svm:支持向量机模型算法库。
- .neural_network:神经网络模型算法库。
- .neightbors:最近邻算法模型库。
实现线性回归算法
下面我们是基于 sklearn 实现线性回归算法,大概可以分为三步,首先从 sklearn 库中导入线性模型中的线性回归算法,如下所示:from sklearn import linear_model其次训练线性回归模型。使用 fit() 喂入训练数据,如下所示:
model = linear_model.LinearRegression() model.fit(x, y)最后一步就是对训练好的模型进行预测。调用 predict() 预测输出结果, “x_”为输入测试数据,如下所示:
model.predict(x_)你可能会感觉 so easy,其实没错,使用 sklearn 算法库实现线性回归就是这么简单,不过上述代码只是一个基本的框架,要想真正的把这台“机器”跑起来,我们就得给它喂入数据,因此准备数据集是必不可少的环节。数据集的整理也是一门专业的知识,会涉及到数据的收集、清洗,也就是预处理的过程,比如均值移除、归一化等操作,如果熟悉 Pandas 的话应该了解, 因此这里不做重点讲解。
1) 准备数据
下面我们手动生成一个数据集,如下所示:# 使用numpy准备数据集 import numpy as np # 准备自变量x,-3到3的区间均分间隔30份数 x = np.linspace(3,6.40) #准备因变量y,这一个关于x的假设函数 y = 3 * x + 2
2) 实现算法
#使用matplotlib绘制图像,使用numpy准备数据集
import matplotlib.pyplot as plt
import numpy as np
from sklearn import linear_model
#准备自变量x,生成数据集,3到6的区间均分间隔30份数
x = np.linspace(3,6.40)
#准备因变量y,这一个关于x的假设函数
y = 3 * x + 2
#由于fit 需要传入二维矩阵数据,因此需要处理x,y的数据格式,将每个样本信息单独作为矩阵的一行
x=[[i] for i in x]
y=[[i] for i in y]
# 构建线性回归模型
model=linear_model.LinearRegression()
# 训练模型,"喂入"数据
model.fit(x,y)
# 准备测试数据 x_,这里准备了三组,如下:
x_=[[4],[5],[6]]
# 打印预测结果
y_=model.predict(x_)
print(y_)
#查看w和b的
print("w值为:",model.coef_)
print("b截距值为:",model.intercept_)
#数据集绘制,散点图,图像满足函假设函数图像
plt.scatter(x,y)
plt.show()
通过线性回归得到的线性函数图像,如下所示:
图1:线性回归函数图像
打印输出结果如下所示:
测试集输出结果: [[14.] [17.] [20.]] w值为: [[3.]] b截距值为: [2.]通过上述代码我们就实现“线性回归”的过程,但是在实际情况中,我们要面临的数据集要复杂的多,绝大多数情况不会这样理想,都会存在一些波动。在生成数据集的代码段内添加以下代码,如下所示:
#准备自变量x,生成数据集,3到6的区间均分间隔30份数 x = np.linspace(3,6.40) #准备因变量y,这一个关于x的假设函数 y = 3 * x + 2 # 添加代码,扰乱点的分布 x = x + np.random.rand(40)利用 NumPy 的 random. rand() 随机生成 0 - 1 之前的波动数值,从而改变数据点的分布情况,如下所示:

图2:修改后的散点分布
虽然做标签散乱分布,但是使用线性回归算法学习依然可以得到线性函数,此时 w 与 b 的输出结果如下所示:
w值为: [[2.68673744]] b截距值为: [0.80154335]绘制最佳拟合直线,程序代码如下:
#使用matplotlib绘制图像,使用numpy准备数据集
import matplotlib.pyplot as plt
import numpy as np
from sklearn import linear_model
#准备自变量x,生成数据集,-3到3的区间均分间隔30份数
x = np.linspace(3,6,40)
#准备因变量y,这一个关于x的假设函数
y=3 * x + 2
x = x + np.random.rand(40)
#准备因变量y,这一个关于x的假设函数
#由于fit 需要传入二维矩阵数据,因此需要处理x,y数据格式,将每个样本信息单独作为矩阵的一行
x=[[i] for i in x]
y=[[i] for i in y]
model=linear_model.LinearRegression()
model.fit(x,y)
#准备测试数据 x_,这里准备了三组,如下:
x_=[[4],[5],[6]]
# 打印预测结果
y_=model.predict(x_)
print(y_)
#查看w和b的
print("w值为:",model.coef_)
print("b截距值为:",model.intercept_)
#数据集绘制,散点图,图像满足函假设函数图像
plt.scatter(x,y)
#绘制最佳拟合直线
plt.plot(x_,y_,color="red",linewidth=3.0,linestyle="-")
plt.legend(["func","Data"],loc=0)
plt.show()
函数图像如下所示:
图3:拟合直线绘制
线性回归步骤
通过上述代码了解了如何使用 Python sklearn 实现线性回归,下面从总整体出发再次审视该算法:掌握线性回归算法的具体步骤。线性回归适用于有监督学习的回归问题,首先在构建线性模型前,需要准备好待输入的数据集,数据集按照需要可划分为训练集和测试集,使用训练集中的向量 X 与向量 Y 进行模型的训练,其中向量 Y 表示对应 X 的结果数值(也就是“参考答案”);而输出时需要使用测试集,输入测试 X 向量输出预测结果向量 Y。
其实线性回归主要解决了以下三个问题:
- 第一,为假设函数设定了参数 w,通过假设函数画出线性“拟合”直线。
- 第二,将预测值带入损失函数,计算出一个损失值。
- 第三,通过得到的损失值,利用梯度下降等优化方法,不断调整 w 参数,使得损失值取得最小值。我们把这个优化参数值的过程叫做“线性回归”的学习过程。
线性回归算法简单,且容易理解,但这并不影响它的广泛应用,比如经济金融领域实现股票的预测,以及著名的波士顿房价预测,这些都是线性回归的典型应有,因此我们要走出一个误区,不要感觉算法简单就不重要,机器学习虽然算法众多,但每一种算法都有其存在的理由,而掌握了线性回归就相当于拿到了算法世界的入场券。
