线性回归:损失函数和假设函数
通过前面内容的介绍,我相信你对线性回归算法已经有了初步的认识。那我们应该如何在一大堆数据中求解出“线性方程呢”比如前面提及的房价预测问题?这种问题才是符合实际应用的。数据样本会散落在“线性方程”的周围(下图 2 所示), 而我们要做就是让线性方程的“直线”尽可能“拟合”周围的数据点。本节我们将从数学角度解析线性回归模型。
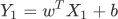
乍一看你可能蒙圈了,记住不用紧张。其实它和 Y=wX + b 是类似的,只不过我们这个标量公式换成了向量的形式。如果你已经学习了 《NumPy 教程》,那么这个公司很好理解,
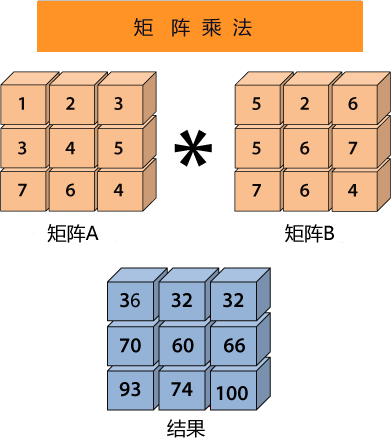
图1:矩阵乘法运算
矩阵 A 的每一行分别与矩阵 B 的每一列相乘,比如 1*5+2*5+3*7 =36 、1*2+2*6+3*6=32、1*6+2*7+3*4=32,即可得出结果的第一行数据。
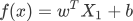
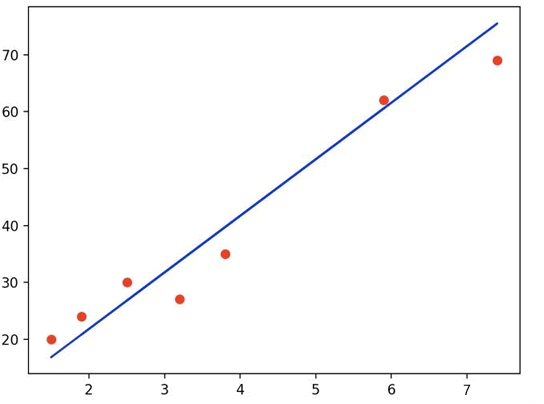
图2:线性回归模型
损失函数就像一个衡量尺,这个函数的返回值越大就表示预测结果与真实值偏差越大。其实计算单个样本的误差值非常简单,只需用预测值减去真实值即可:
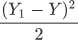
公式是求“距离”因此要使用平方来消除负数,分母 2 代表样本的数量,这样就求得单样本误差值。当我们知道了单样本误差,那么总样本误差就非常好计算了:
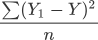 最后,将假设函数带入上述损失函数就会得到一个关于 w 与 b 的损失函数(loss),如下所示:
最后,将假设函数带入上述损失函数就会得到一个关于 w 与 b 的损失函数(loss),如下所示:
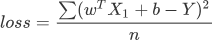
在机器学习中使用损失函数的目的,是为了使用“优化方法”来求得最小的损失值,这样才能使预测值最逼近真实值。
在上述函数中 n、Y、X1 都是已知的,因此只需找到一组 w 与 b 使得上述函数取得最小值即可,这就转变成了数学上二次函数求极值的问题,而这个求极值的过程也就我们所说的“优化方法”。关于如何求极值会在下一节做详细介绍。
假设函数
通过前面知识的学习,我们知道假设函数是用来预测结果的。前面讲述时为了让大家更容易理解“线性回归”,我们以“直线方程”进行了类比讲解,然而线性方程并不等同于“直线方程”,线性方程描绘的是多维空间内的一条“直线”,并且每一个样本都会以向量数组的形式输入到函数中,因此假设函数也会发生一些许变化,函数表达式如下所示: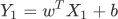
乍一看你可能蒙圈了,记住不用紧张。其实它和 Y=wX + b 是类似的,只不过我们这个标量公式换成了向量的形式。如果你已经学习了 《NumPy 教程》,那么这个公司很好理解,
Y1仍然代表预测结果, X1表示数据样本, b表示用来调整预测结果的“偏差度量值”,而wT 表示权值系数的转置。矩阵相乘法是一个求两个向量点积的过程,也就是按位相乘,然后求和,如下所示:
图1:矩阵乘法运算
矩阵 A 的每一行分别与矩阵 B 的每一列相乘,比如 1*5+2*5+3*7 =36 、1*2+2*6+3*6=32、1*6+2*7+3*4=32,即可得出结果的第一行数据。
转置操作的目的是为了保证第一个矩阵的列数(column)和第二个矩阵的行数(row)相同,只有这样才能做矩阵乘法运算。
您也可以将假设函数写成关于 x 的函述表达式,如下所示: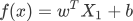
损失函数
我们知道,在线性回归模型中数据样本散落在线性方程的周围,如下图所示:
图2:线性回归模型
损失函数就像一个衡量尺,这个函数的返回值越大就表示预测结果与真实值偏差越大。其实计算单个样本的误差值非常简单,只需用预测值减去真实值即可:
单样本误差值 = Y1 - Y但是上述方法只适用于二维平面的直线方程。在线性方程中,要更加复杂、严谨一些,因此我们采用数学中的“均方误差”公式来计算单样本误差:
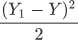
公式是求“距离”因此要使用平方来消除负数,分母 2 代表样本的数量,这样就求得单样本误差值。当我们知道了单样本误差,那么总样本误差就非常好计算了:
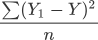
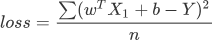
在上述函数中 n、Y、X1 都是已知的,因此只需找到一组 w 与 b 使得上述函数取得最小值即可,这就转变成了数学上二次函数求极值的问题,而这个求极值的过程也就我们所说的“优化方法”。关于如何求极值会在下一节做详细介绍。
