图的十字链表存储结构
前面介绍了图的邻接表存储法,本节继续讲解图的另一种链式存储结构——十字链表法。
与邻接表不同,十字链表法仅适用于存储有向图和有向网。不仅如此,十字链表法还改善了邻接表计算图中顶点入度的问题。
十字链表存储有向图(网)的方式与邻接表有一些相同,都以图(网)中各顶点为首元节点建立多条链表,同时为了便于管理,还将所有链表的首元节点存储到同一数组(或链表)中。
其中,建立个各个链表中用于存储顶点的首元节点结构如图 1 所示:

图 1 十字链表中首元节点结构示意图
从图 1 可以看出,首元节点中有一个数据域和两个指针域(分别用 firstin 和 firstout 表示):
注意,存储图的十字链表中,各链表中首元节点与其他节点的结构并不相同,图 1 所示仅是十字链表中首元节点的结构,链表中其他普通节点的结构如图 2 所示:

图 2 十字链表中普通节点的结构示意图
从图 2 中可以看出,十字链表中普通节点的存储分为 5 部分内容,它们各自的作用是:
比如说,用十字链表存储图 3a) 中的有向图,存储状态如图 3b) 所示:
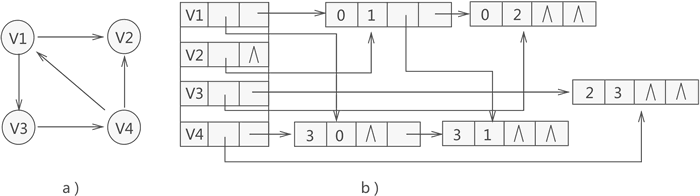
图 3 十字链表存储有向图示意图
拿图 3 中的顶点 V1 来说,通过构建好的十字链表得知,以该顶点为弧头的顶点只有存储在数组中第 3 位置的 V4(因此该顶点的入度为 1),而以该顶点为弧尾的顶点有两个,分别为存储数组第 1 位置的 V2 和第 2 位置的 V3(因此该顶点的出度为 2)。
对于图 3 各个链表中节点来说,由于表示的都是该顶点的出度或者入度,因此没有先后次序之分。
图 3 中十字链表的构建过程转化为 C 语言代码为:
与邻接表不同,十字链表法仅适用于存储有向图和有向网。不仅如此,十字链表法还改善了邻接表计算图中顶点入度的问题。
十字链表存储有向图(网)的方式与邻接表有一些相同,都以图(网)中各顶点为首元节点建立多条链表,同时为了便于管理,还将所有链表的首元节点存储到同一数组(或链表)中。
其中,建立个各个链表中用于存储顶点的首元节点结构如图 1 所示:

图 1 十字链表中首元节点结构示意图
从图 1 可以看出,首元节点中有一个数据域和两个指针域(分别用 firstin 和 firstout 表示):
- firstin 指针用于连接以当前顶点为弧头的其他顶点构成的链表;
- firstout 指针用于连接以当前顶点为弧尾的其他顶点构成的链表;
- data 用于存储该顶点中的数据;
由此可以看出,十字链表实质上就是为每个顶点建立两个链表,分别存储以该顶点为弧头的所有顶点和以该顶点为弧尾的所有顶点。
注意,存储图的十字链表中,各链表中首元节点与其他节点的结构并不相同,图 1 所示仅是十字链表中首元节点的结构,链表中其他普通节点的结构如图 2 所示:

图 2 十字链表中普通节点的结构示意图
从图 2 中可以看出,十字链表中普通节点的存储分为 5 部分内容,它们各自的作用是:
- tailvex 用于存储以首元节点为弧尾的顶点位于数组中的位置下标;
- headvex 用于存储以首元节点为弧头的顶点位于数组中的位置下标;
- hlink 指针:用于链接下一个存储以首元节点为弧头的顶点的节点;
- tlink 指针:用于链接下一个存储以首元节点为弧尾的顶点的节点;
- info 指针:用于存储与该顶点相关的信息,例如量顶点之间的权值;
比如说,用十字链表存储图 3a) 中的有向图,存储状态如图 3b) 所示:

图 3 十字链表存储有向图示意图
拿图 3 中的顶点 V1 来说,通过构建好的十字链表得知,以该顶点为弧头的顶点只有存储在数组中第 3 位置的 V4(因此该顶点的入度为 1),而以该顶点为弧尾的顶点有两个,分别为存储数组第 1 位置的 V2 和第 2 位置的 V3(因此该顶点的出度为 2)。
对于图 3 各个链表中节点来说,由于表示的都是该顶点的出度或者入度,因此没有先后次序之分。
图 3 中十字链表的构建过程转化为 C 语言代码为:
#define MAX_VERTEX_NUM 20
#define InfoType int//图中弧包含信息的数据类型
#define VertexType int
typedef struct ArcBox{
int tailvex,headvex;//弧尾、弧头对应顶点在数组中的位置下标
struct ArcBox *hlik,*tlink;//分别指向弧头相同和弧尾相同的下一个弧
InfoType *info;//存储弧相关信息的指针
}ArcBox;
typedef struct VexNode{
VertexType data;//顶点的数据域
ArcBox *firstin,*firstout;//指向以该顶点为弧头和弧尾的链表首个结点
}VexNode;
typedef struct {
VexNode xlist[MAX_VERTEX_NUM];//存储顶点的一维数组
int vexnum,arcnum;//记录图的顶点数和弧数
}OLGraph;
int LocateVex(OLGraph * G,VertexType v){
int i=0;
//遍历一维数组,找到变量v
for (; i<G->vexnum; i++) {
if (G->xlist[i].data==v) {
break;
}
}
//如果找不到,输出提示语句,返回 -1
if (i>G->vexnum) {
printf("no such vertex.\n");
return -1;
}
return i;
}
//构建十字链表函数
void CreateDG(OLGraph *G){
//输入有向图的顶点数和弧数
scanf("%d,%d",&(G->vexnum),&(G->arcnum));
//使用一维数组存储顶点数据,初始化指针域为NULL
for (int i=0; i<G->vexnum; i++) {
scanf("%d",&(G->xlist[i].data));
G->xlist[i].firstin=NULL;
G->xlist[i].firstout=NULL;
}
//构建十字链表
for (int k=0;k<G->arcnum; k++) {
int v1,v2;
scanf("%d,%d",&v1,&v2);
//确定v1、v2在数组中的位置下标
int i=LocateVex(G, v1);
int j=LocateVex(G, v2);
//建立弧的结点
ArcBox * p=(ArcBox*)malloc(sizeof(ArcBox));
p->tailvex=i;
p->headvex=j;
//采用头插法插入新的p结点
p->hlik=G->xlist[j].firstin;
p->tlink=G->xlist[i].firstout;
G->xlist[j].firstin=G->xlist[i].firstout=p;
}
}
提示,代码中新节点的插入采用的是头插法。
