首页 > 编程笔记
回溯算法
在图 1 中找到从 A 到 K 的行走路线,一些读者会想到用穷举算法(简称穷举法),即简单粗暴地将从 A 出发的所有路线罗列出来,然后逐一筛选,最终找到正确的路线。
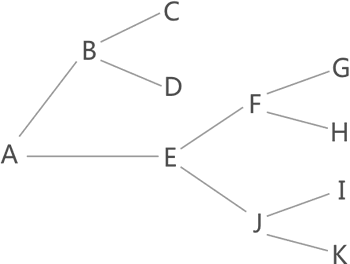
图 1 找从A到K的行走路线
图 1 中,从 A 出发的路线有以下几条:
本节要讲的回溯算法和穷举法很像,它也会把所有可能的方案都查看一遍,从中找到正确答案。不同之处在于,回溯算法查看每种方案时,一旦判定其不是正确答案,会立即以“回溯”的方式试探其它方案。
所谓“回溯”,其实就是回退、倒退的意思。仍以图 1 为例,回溯算法查找从 A 到 K 路线的过程是:
回溯算法采用“回溯”(回退)的方式对所有的可行方案做出判断,并最终找到正确方案。和穷举法相比,回溯算法的查找效率往往更高,因为在已经断定当前方案不可行的情况下,回溯算法能够“悬崖勒马”,及时转向去判断其它的可行方案。
用回溯算法解决的经典问题有 N皇后问题、迷宫问题等,我们会在后续章节给大家做详细地讲解。

图 1 找从A到K的行走路线
图 1 中,从 A 出发的路线有以下几条:
A-B-C
A-B-D
A-E-F-G
A-E-F-H
A-E-J-I
A-E-J-K
本节要讲的回溯算法和穷举法很像,它也会把所有可能的方案都查看一遍,从中找到正确答案。不同之处在于,回溯算法查看每种方案时,一旦判定其不是正确答案,会立即以“回溯”的方式试探其它方案。
所谓“回溯”,其实就是回退、倒退的意思。仍以图 1 为例,回溯算法查找从 A 到 K 路线的过程是:
- 从 A 出发,先选择 A-B 路线;继续从 B 出发,先选择 B-C 路线;到达 C 点后发现无路可选,表明当前路线无法达到 K 点,该算法会立刻回退到上一个节点,也就是 B 点;
- 从 B 点出发,选择 B-D 路线,达到 D 点后发现无法到达 K 点,该算法再回退到 B 点;
- 从 B 点出发已经没有新的线路可以选择,该算法再次回退到 A 点,选择新的 A-E 路线;
- 继续以同样的方式测试 A-E-F-G、A-E-F-H、A-E-J-I 这 3 条线路后,最终找到 A-E-J-K 路线。
回溯算法采用“回溯”(回退)的方式对所有的可行方案做出判断,并最终找到正确方案。和穷举法相比,回溯算法的查找效率往往更高,因为在已经断定当前方案不可行的情况下,回溯算法能够“悬崖勒马”,及时转向去判断其它的可行方案。
回溯算法的应用场景
回溯算法经常以递归的方式实现,用来解决以下 3 类问题:- 决策问题:从众多选择中找到一个可行的解决方案;
- 优化问题:从众多选择中找到一个最佳的解决方案;
- 枚举问题:找出能解决问题的所有方案。
用回溯算法解决的经典问题有 N皇后问题、迷宫问题等,我们会在后续章节给大家做详细地讲解。
